A note to my readers
I make a conscious effort to avoid arbitrary targets – it seems nonsensical to center your appreciation of a loved one on the 14th of February, to delay making a positive change because the Gregorian calendar has not reset or to be more charitable once a year due to a festival from a religion you are not a member of. That said, there is a relative amount of calm in the weeks surrounding the holidays that gives the opportune moment for self-evaluation. With regard to Rationalising the Universe I am pleased with the progress we have made and continue to be astonished with the number of writers from all disciplines who engage with the site. I offer no great change in direction for a site which is not broken – but rather propose some refinements.
This site was set up for a number of reasons – but the overarching aim was to bask in the glory of science for nothing but pleasure. Over the last few months I have written increasingly about the forefronts of theoretical and particle physics – something of great interest to us all, but as caveat-ed I have more questions than answers in these areas. Whilst this is a noble pursuit, I fear I am being permanently seduced while avoiding the foundations of mankind’s knowledge; popularizing popular science is actually fairly easy, it is popularizing the bread and butter which requires a certain zeal. I propose over the coming year, very occasionally we cover an essential area in any undergraduate physicists toolkit. This will, I hope, be (slightly) more interesting than the average textbook. This is not to say musings on the forefront of theoretical physics are suspended – they will remain the main event, interspersed with essential physics to ensure we do battle properly equipped. This may be a little painful I am afraid.
Thank you for your continued interest and support in the site, I hope you choose to stay reading Rationalising the Universe through 2017
– Joe
Simple harmonic motion
What an arrogant title – unfortunately the name is too embedded in science for us to be able to make any changes to it, so whilst you may not find this topic simple, we will call it simple harmonic motion, or SHM for brevity. I often like to start with the dictionary definition of a word or phrase before uncovering the detail, which for SHM we have;
simple harmonic motion
noun
-
oscillatory motion under a retarding force proportional to the amount of displacement from an equilibrium position.
Forces like this can be modeled very neatly using mathematics, since we have a force which depends only upon the position of the particle. We will consider the case of a spring, with one end attached to a fixed end and the other free to move with a particle attached to the end of it. The set up can be seen in the diagram below.

All I intend to do today is to derive from first(ish) principles an equation which will allow us to model the motion of the particle. Note that the above diagram is showing phases of time – the only motion we have is in the vertical direction. This is called the j-direction which in the below formulas, for now you will see denoted j with a hat (^) on it. This is not really any different to saying upwards, but what it actually means is a unit vector in the vertical direction which we have defined. Generally when you try to model anything which has classical motion you first need to consider the forces. There are two forces here – the weight of the particle and the spring force.
Dealing with the weight first, the weight of any object is the mass of the object multiplied by the acceleration due to gravity. It is this second part which changes depending on the gravitational field you find yourself in – hence why you can say you weigh less on the moon than on Earth. If we have expressed the positive j-direction as vertically downwards, then the weight of the particle can be expressed as follows;

Now we move onto the spring force – the spring force obeys a law known as Hooke’s law. Often when you see formulas written down they seem very difficult to construct – actually they are just the result of people who mess around with springs and know how to draw graphs. From experiment, it turns out the force a spring exerts is proportional to the deformation of the spring (which may be compressed or stretched) by a constant known as the stiffness of the spring (k). The force is directed towards the center of the spring – which leaves us with an initial dilemma for our model; should we take the force as being in the positive or negative j-direction, since it can be both? Spoiler – it makes no difference. So we can set up our spring force as follows, where x is the position of the particle.

Note that the term l with a subscript 0 is the natural length of the spring. That was a little dry but now we are in business, we have forces giving rise to motion of a particle which can only mean Newton. We want to express the motion of the particle on the spring as F=ma, however there is an issue in that a introduces a further variable. However let us define the x-direction to be vertical (I know this isn’t a Cartesian set up, but it’s my model so deal with it). Now the position of the particle at any moment in time can be modeled as some function of t, say x(t). Since velocity is the rate of change of position, and acceleration is the rate of change of velocity I may denote the acceleration as the second derivative of x, or in applied mathematics notation x with two dots above it. A derivative is simply the rate of change – so I am taking the rate of change twice of x. This means I can rewrite our famous F=ma as;

The next logical step from here is to replace F with the forces we have define above. All of a sudden I am going to drop my unit vector j – this is okay. What I have done is reached a point where I have realized I only have j-components so resolved in this direction (see note 1), so I can just consider these forces with the unit vector implied.

Now using the above I consider only the last two terms, which I expand out and collect all x-terms on one side with all constant terms on the other side. This gives;

This is a differential equation in x – an equation that links the derivatives of x. All other terms here are constants, so really once we have set up a real system these will just be numbers. If you are really mathematically minded, or just like jargon, what I have constructed is a second order constant coefficient in-homogeneous differential equation. The solution to a differential equation is a function which satisfies the equation – i.e some kind of mathematical expression that when we substitute it into the above, the equality is satisfied. I have illuminated more of the logic in the notes for those who are interested, but the first stage is to solve the equation as if the right hand side were to equal zero (which is called the complimentary homogeneous function). To do this I have defined a new constant omega such that;
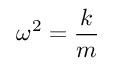
Now an equation which will satisfy my differential equation if the right hand were to be zero is as follows (note 2);
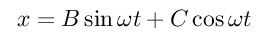
Here B and C are arbitrary constants. Next we need to deal with the right hand side – since the right had side is not actually zero we need to add a term to the above solution to make it work. In fact what we need to add is the equilibrium position of the particle, multiplied by the stiffness of the spring. Please see note 3 for further discussion – but if you think about what is happening; a particle oscillating around an equilibrium position this hopefully will roughly”feel right”. This gives us the following final general solution.
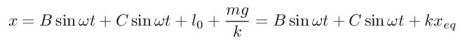
And there we have our solution – we can define the position of a particle, oscillating in harmonic motion from a spring with the above equation. We would need to know the stiffness of our spring, the mass of the particle and the natural length of the spring in order to quantify omega, k and x-eq. Following on from this, we would need an initial condition in order to remove the arbitrary constants B and C – this would look something like initially the particle is released from rest at position x = 0.1m for example. This will be specific to the model we look at.
Why do I care?
Being able to model the motion of particles under forces is central to all of Physics; and it is entirely implausible to think that one might go on to model complex quantum mechanical systems if simple classical skills have not been gained. That is not to say the above skills will be directly used (they generally will not), but the mindset of the Physicist (and the Mathematician) is to be able to take a real world situation, express as much of this information mathematically and produce a model which is a close match to real world results. This is a most wonderful thing. This article goes into a little more depth around the applications of harmonic motion.
Finally – my apologies for this dense technical post. Please ask anything you have not understood, I can give confident answers on this topic; my next few posts will be light and much less technical.
Notes:
- When you consider motion in one direction, you will only have a resultant force in that direction. If you had a resultant force in another direction you would have motion in more than one direction – so by construction we do not. That isn’t to say we don’t have forces in other directions – say a train moving along a straight track- we have the weight and the normal reaction force vertically and the thrust and resistive forces horizontally, however the vertical forces are equal and opposite, so we can consider only the horizontal to model the motion.
- In order to solve this differential equation we first consider the auxiliary equation which is found as;
 Clearly then lambda is equal to the square root of -omega as defined previously which gives my roots as +/- omega i. When we have complex roots a +/- bi, we can construct a solution in the following form
Clearly then lambda is equal to the square root of -omega as defined previously which gives my roots as +/- omega i. When we have complex roots a +/- bi, we can construct a solution in the following form  Where in this case we have a=0, hence this term drops away to 1, with b equal to omega.
Where in this case we have a=0, hence this term drops away to 1, with b equal to omega. - The next step to solve an in-homogeneous differential equation is to take a particular integral and add it to the equation – generally this is done by taking a trial term which matches the right hand side in form, plugging it into the equation and equating coefficients. In this example it is actually very easy – if I take x = K, some constant since I have a constant on the right hand side, when I plug this into my differential equation I am left with
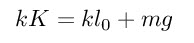 Which does not take much rearranging to give me the required solution above. The solution to an inhomogenous differential equation is the sum of the solution to the homogeneous complimentary function plus the particular integral – by the principle of superposition. In order to make the conceptual leap to this being k times the equilibrium position, simply resolve all forces where the is no resultant force. Ask me if you get stuck.
Which does not take much rearranging to give me the required solution above. The solution to an inhomogenous differential equation is the sum of the solution to the homogeneous complimentary function plus the particular integral – by the principle of superposition. In order to make the conceptual leap to this being k times the equilibrium position, simply resolve all forces where the is no resultant force. Ask me if you get stuck. - By convention all forces are written in bold. This is to indicate they are vector quantities. When you do them by hand you should underline them
- Unit vectors are also denoted in bold, but have a ^ on them to denote their significance as being of magnitude 1 in a specified direction.
- Using these techniques one can very easily extend the model to any particle moving with simple harmonic motion – the results will have minor changes by there is no need to restrict to this spring example. An easy natural next step is to consider a horizontal spring – the results of this are quite similar, but this applies to all manner of situations. Damping, resonance and forced vibrations are all natural extension topics to increase your modelling capabilities.
- Often in textbooks you will see the solution written the other way round, with the cosine function first taking the B coefficient. I don’t know what made me write it this way – but truly it makes no difference.

While I studied Physics, we went the traditional way. You provided a fresh look to the concepts and the mathematical basis thereunder. But for the beginners/novices, it’s bit technical. May be simplified for later posts.
LikeLiked by 1 person
I agree with you entirely – this topic would be too complex for a beginner to understand it requires some mathematical knowledge to comprehend. Posts this complex will be very rare I assure you!
LikeLiked by 1 person
What can u lay on the table about quantum physics?
LikeLike
You may find these posts of interest with regard to Quantum:
Thanks for reading
Joe
LikeLike
Thanks
LikeLike
Could the universe be in a state of simple harmonic motion? currently expanding then contracting, then expand again?
LikeLike
An interesting idea, and one that is totally possible of course – I wouldn’t be bold enough to just say outright no… but it seems difficult to give much credit to without a good theory of what the force is keeping the universe in SHM – when something moves with SHM we have a force which is responsible for the motion, so say a spring force or the tension in the pendulum… I just can’t imagine any force that could support the movement of our universe in a state of SHM. That said – there is so much we don’t yet know it would be silly to take anything off the table!
LikeLike
I would be reading the rest of the post slowly and with deep interest. However, I would like to congratulate you on the opening paragraph of this post. Exactly, why seek some pretext to do something positive or good? We must come out of self imposed barriers and make an effort to free ourselves and others of this burden. This very moment is a moment at hand. Be the change now!
Thank you so much for those words. “Bow”
LikeLiked by 2 people
Thank you very much! I appreciate this post is likely to baffle many – but I have come to the conclusion we must all try to digest a balanced diet of what we want and what we need. This post is a difficult one and they will not be a regular feature – however as I said I do think they are essential! Thank you very much for your kind words.
Joe
LikeLike
May I take the liberty of offering a suggestion? I follow your blog religiously and it is one of my favourite blogs … But when you deal with any concept, I suggest you to simplify it further to keep the readers engaged. That way, not only are they able to marvel at physics but even admire its simplicity and everyday application.
Keep writing and enthralling us … Much love Sugarsatchet
LikeLiked by 3 people
Thank you for reading and for your suggestion – I will endeavor to achieve this. I have two inner conflicts I find difficult to balance;
1. To present science that interests people whilst not ignoring essential science
2. Simplifying matters without letting the wordcount grow too high leaving readers disengaged
You will be pleased to know however a post of this complexity will be issued very rarely and I am going to create a new flag “Technical”. The next post will be back to punchy, short posts of greater simplicity you have my word.
Thank you very much for reading,
Joe
LikeLiked by 3 people
Reading your blog posts helps me understand this world and its phenomena in a more lucid manner. Love it. Keep at it
LikeLiked by 3 people
Terrific way to start 2017 with a swing Joe 🙂 So Very Happy New Year to you and Mekhi.
I wondered if you might deal with SHM, as I’d attempted a brief overview almost 5 yrs ago today in my early blogging in a post on biblical, historical and financial cycles; and much later in a basic mathematical outline for considering the nature of time which, imho, is an essential for Bible students to appreciate more deeply.
In case you/anyone may have time and inclination to check such non-tech posts, they’re at http://wp.me/p1Y1yB-ni and http://wp.me/P1Y1yB-6u0 respectively.
LikeLike
Hi Richard – thank you very much! A bit of a heavy start to the year I know but I am glad you enjoyed it; I had been toying with the idea for a while it is a little technical and a little less…fun! 5 years ago – very impressive! We here at Rationalising the Universe are only 15 months old; feeling very young indeed. It is amazing how much motion you really can describe in this way so I would agree with you in the sense that it is a very powerful tool. Thank you very much for the links I will give them a read.
LikeLiked by 1 person
This is, in no way, a criticism of your effort or presentation but, as I have indicated elsewhere, the algebraic representation of variables is a major obstacle to me as (probably) a victim of dyscalculia and just the attempt to transfer reality into a formula or equation indicating variable relationships of dynamic processes gives me the willies. I get mentally involved with the unbalanced vertical problem of a mass accepting gravity on the way down and fighting the spring tension on the way up so the sine pattern is flattened on top and extended on the bottom. If the vibration were to be in a horizontal spring there would be no distortion and actually this variation is probably negligible in actuality. I do not “read” formulas as I do words and sentences which is a crippling lack in scientific disciplines where the interplay of variables and constants is the lingua franca of the communications. I apologize for my lacks and will do my best to follow your efforts.
LikeLiked by 1 person
I did think when I hit post this one might not be your favorite Jiisand! Not to worry anyhow – this sort of post is likely to be at most 2-3 a year, the next post coming up is in antimatter which I think you will particularly enjoy. You shouldn’t do yourself a disservice though – you have a way of understanding and appreciating the motion we describe in this instance which need not be the same as the one presented above. Indeed both the horizontal and the vertical would have no motion if initially started from rest in their “natural” position. The motion arises when we introduce a distortion – those humans messing around again!
LikeLike
In my queasy relationship with quantity I do not reduce my reality to symbols. I create a spring in my mind and hang a weight on it and I can feel and see the forces involved and can watch how that weight bounces up and down and drags a pen across a long strip of paper. I don’t figure out how it behaves, I just watch what happens. Naturally, since reality, for me, is a personal fantasy as it is with everybody, whether the real weight and spring behaves the same way is quite questionable.
LikeLiked by 1 person
It would be nice, if you told the reader why the ratio of the Stiffness to mass is
 …the reason is both mathematical and physical. From the requirement of the dimensional equality, the physical part is satisfied [
…the reason is both mathematical and physical. From the requirement of the dimensional equality, the physical part is satisfied [ ]. For the case of mathematical reasoning, all I can think of is that since the equation of motion is of the second order, the constant is taken to be square so that when we take the characteristic equation, the roots comes out to be without the square root sign. What do you think?
]. For the case of mathematical reasoning, all I can think of is that since the equation of motion is of the second order, the constant is taken to be square so that when we take the characteristic equation, the roots comes out to be without the square root sign. What do you think?
LikeLiked by 1 person
What a wonderful question! Firstly, how delightful to see someone call 1/sec^2 satisfy the physical reality. I agree with you entirely the sinusoidal functions are deeply embedded in my reality, however I am not sure that everyone would see it that way! If you think about it we defined this constant as being the stiffness of the spring; for the value to be less than zero you either need a negative mass, or a negative stiffness constant. Negative mass is not something deal with, and by its very definition the stiffness constant must be positive (even if you let it be negative you can make it positive with a suitable origin). I think if we were to start to go down the route of negative omegas we would have a damping which is something different, and modeled with exponents. Does that make sense? I think we would have actually chosen to define omega differently, it would of just generated an ugly solution
LikeLiked by 1 person
Thanks Jo!
Negative mass would absolutely absurd in the classical world. However, in the quantum world things get interesting. If you think about it, the very idea of negative energy solutions [E=m] lead Dirac to boldly predict the so called anti-particles. However, classically the mass is strictly > 0. This leaves us with the stiffness constant. By definition, the stiffness constant is Force/displacement (one dimensional case). If the stiffness constant becomes negative i.e. k<0; it would imply either F is negative or displacement is. From what we know, Force and displacement are opposite for the case of a disturbed spring ( i.e. from its equilibrium value). Now, Suppose that the k is < 0, then the case for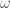 is
is
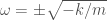

or
The frequency of the system is purely imaginary. This changes the solution from sinusoidal to exponential types. Hence, you are justified in calling the damped solutions. This concept of SHM is very important and is at the heart of classical as well as modern physics.
LikeLike
An interesting idea – however the one subtlety in this case is I think the unit vector directed towards the center of the spring in this case of negative stiffness would also reverse – so I think we would get back to the original solution. What we have done however is come full circle to a force which resists the motion of the force – which is the damping constant which changes in line not with the displacement but with the rate of change of displacement from the origin (velocity). So there the roots give us a solution with the sinusoidal motion being damped by an exponential factor. I agree with you totally SHM is very important indeed – it’s what made me decide to give it it’s own post, even though it isn’t the most glitsy of topics
LikeLiked by 1 person
simple harmonic Universe
Seems to be an interesting read.
LikeLike
You’re blowing my mind!
LikeLiked by 1 person
Thank you very much!
LikeLiked by 1 person
I enjoy your posts but take my fun away and I shall be forced to find myself a biologist instead…they know how to have a good time 😉
Seriously, it is your blog but this might be a little complex for some. Fun science with every day relatable content is far easier to absorb. I guess it is a question of whom you are trying to reach out to…those who already know and can appreciate your turn of phrase or those who you would like to bring in and give an understanding of a topic you love 🙂
Now, do I duck the chalk or is it just an hour’s detention? *smiles*
LikeLike
Thank you for your visit! No chalk will be thrown, I don’t think it’s allowed these days! Don’t fear – I will be writing at most two of these a year – not only are they hard for the reader they are also tougher for me to pull together. My aim is to keep the blog as it was before, but just on the odd occasion add a post for those who want to add a little mathematical rigor. Look out for my next post – you will enjoy it I promise. Stay away from the plant people.
LikeLiked by 1 person
Perhaps I should refrain from this single note in my discourse but my discomfort and even fear of mathematics has been a prime tragedy in my life. I feel like a crippled bird who watches others soar through wonderful immense spaces and at best I can scratch my way up a tall tree and watch the distant Moon at night. As scientists have long known the disciplined arrays of armies of numbers have , at least to the means of human thought, touched the unknown in ways that our deceptive and delightful senses are dwarfed by the depths of reality. Nevertheless I keep chirping and leaping an inch or so towards the clouds and remain amazed as they majestically proceed across the endless sky.
LikeLike
I like your article, very inspiring and thank you for your post
LikeLiked by 1 person
I can see the formulas and even though I loved them back in my uni days (statistics was my favourite subject, sad eh?) I have no interest in them now – but that’s just me and this ain’t my blog.
I would like to say thank you – I really appreciate how most of your blog posts (and Mekhi’s) simplify physics and take us beyond the text book approach for a fresh, engaging perspective. I actually think when you take a complex topic and make it simple for the readers it takes an extra level of knowledge.
Thanks for the good work!
LikeLike
No problem at all and please do stay tuned for the next post – which is a lighthearted exploration of antimatter with not a formula in sight! You will enjoy I assure you!
LikeLiked by 1 person
Yay! Can’t wait!
LikeLiked by 1 person
A bit too mathematical for me , anything beyond simple algebra floors me, but I have a few questions. Am I correct in thinking energy is past back and forth from the spring to the weight? What prevents this process from perpetual activity ? Is it air resistance? Is this oscillation the same in a mathematical sense as a bouncing rubber ball? Is mechanical energy rather like heat and if it cannot escape it is trapped in perpetual oscillations? In the same way heat is trapped in a vacuum flask? No doubt the math enables you to calculate the speed of these oscillations or number per second , does this lead on to finding how fast atoms or molecules vibrate in a solid?
LikeLiked by 1 person
Hi Kertsen – great questions!
There are forces, and there is energy. The particle has kinetic energy and it has potential energy – in a “model” system there will be an exact trade off between motion and potential energy giving perpetual oscillations. In reality, there are forces resisting the motion – damping the system such as air resistance or friction within the spring system.
Bouncing the ball does have its similarities – we have gravity acting on the spring as before; the slight difference here is we have a new force which is governed by displacement of the base of the bouncing ball but only when it is in contact with the floor. The second it leaves the floor it is at its maximum velocity and is decelerating. In the absence of any restive forces this would continue in perpetuity very similar in nature. This is very hard to imagine of course since a ball generates sound and heat when it hits almost any surface.
But yes you are right with mechanical energy – if we can prevent any energy from being lost from the system then we would in theory have perpetual motion.
The math does enable it, very simple actually the frequency is 1/2pi multiplied by omega as defined in the article. You can indeed derive a simple harmonic equation to model the vibration of atoms in a solid
LikeLike
May the good in people last long on the Internet for future generations. Thank you for being a part of why the Internet is great.
LikeLiked by 1 person
Thank you very very much! We are both very grateful to have you reading
LikeLike
Sometimes, late at night or early in the morning sleep for me becomes evasive and that bouncing spring got tangled in my thinking. I started to wonder if the spring tension could be non-uniform along the length of spring and, like a sound wave traveling down an enclosed tube of air or even a voltage traveling down a wire could a spring carry information down a long length with tension variations? A rubber band tied to a diaphragm or a string tied to the bottom of a paper cup might also be equivalent. Just a weird thought about how the spring bounce might be modified.
LikeLike
In equilibrium the spring force cannot be non-uniform however in the non-equilibrium case in the analysis we deal with the overall effect the spring has on the particle. As to if the spring force is uniform… I am not sure but my suspicions are that you are correct in the analogy of a sound wave. This seems logical – but I believe it leaves the overall model unchanged
LikeLike
Thanks for the consideration. It was an odd thought about informational transmission. In the same manner I thought about a beam of light that might change in color along its length somewhat in the way FM radio modulates frequency to carry information. A long spring might vary the proximity of its coils along its length for informational transmission. My mind sometimes wanders in peculiar pathways.
LikeLike
Pingback: When 2 become 1 | Rationalising The Universe·
Pingback: When 2 become 1·
Although I am late on the scene and mathematically have all the ambitions of a clam in training to enter the Olympic high jump competition I still am fascinated by harmonic motion and discovered at https://www.google.fi/search?q=laws+of+resonant+harmonics&ie=utf-8&oe=utf-8&client=firefox-b&gfe_rd=cr&ei=wbGNWKGBMouA8QeqkK3ACQ
many of the peculiarities of harmonic resonance and the graphic delights of Lissajous patterns which are an extension of this introduction.
I have also started to wonder if some extraordinary relationship of resonant harmonics might have some possibilities in the most mysterious quantum entanglement which seems to violate all the accepted concepts of time and space.
LikeLike
Wow amazing
LikeLike
Thank you very much!
LikeLike
Pingback: basit harmonik hareket – simple.·